For some reason I cannot fully understand, certain types of serial decompositions of Mueller matrices became quite popular among experimentalists. I am talking about the polar decomposition and the Lu-Chipman decompositions. These matrix decompositions allow to decompose a matrix in a series of a retarder, a diattenuator and, eventually, also a depolarizer. Of course matrix multiplication is not commutative and, therefore, these decompositions are not unique. In general my advise would be to avoid serial decomposition of a Mueller matrix unless you have reasonable suspects that the investigated sample really corresponds to a certain succession of a retarder, diattenuator and a depolarizer. And, as a experimentalist, I can say that this will rarely happen.
In my view, the decompositions of the Mueller matrix based on a continuous medium have a much more general applicability and they should be the best choice for unknown samples. Some years ago we published the analytic equations find the results straightforwardly (Optics letters 35.4 (2010): 559-561 and Optics Letters 35.20 (2010): 3525-3525). However such equations apply to a Mueller-Jones matrix (non-depolarizing Mueller matrix) and I am aware that some people is having difficulties to apply them to general (depolarizing) Mueller matrix. In the papers that procedure was outlined, but anyway I upload here the code for such calculation, to clarify how the results should look like.
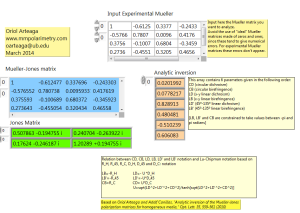
I upload a Labview library program that does such interpretation (run the vi “MManalysis.vi”. I also upload the same program but as an application in case there is anybody that cannot use Labview. Once you open it you will find something like this:
Labview Library www.mmpolarimetry.com/MManalysis%20Labview%202012.llb
Application www.mmpolarimetry.com/MManalysis.rar
You only need to write down a Mueller matrix (preferably an experimental one) and the program will give the closest Mueller-Jones and Jones matrices (in the Cloude sense) and the 6 independent parameters that better define your media (CD,CB,LD,LB,LD’ and LB’). **
———–
**. This analytic interpretation of continuous medium coincides 100% with the Log/differential method of analysis of Mueller matrices for nondepolarizing media, and it is computationally faster and numerically more robust. In the presence of strong depolarization there will be differences among both techniques, but that will be a topic for another day.