Circular dichroism (CD) is the differential absorption of left- and right- circularly polarized light. Nowadays it is a technique ubiquitously used in chemistry and biotechnology for the conformational analysis of biomolecules. An apparatus for CD measurement is present in almost every research center in world working in these fields. Unfortunately this technique is too often not well understood and vendors of CD instruments have not helped their customers to understand the intrinsic limitations of their apparatus in some measurements. Here I will try to explain in a very affordable way the problematic.

The intuitive approach to measure circular dichroism is to illuminate the sample alternatively with left- and right- circularly polarized light, and then measure at the detector which is the difference of transmittance or absorbance of the sample for both types of illumination  (see for example the tutorials at Jasco, and Applied Photophysics). Sounds easy and this is more or less what commercial CD instruments do. But in many occasions it is wrong!.

The basic optical design of all commercial CD instruments (also synchrotron CD beamlines) has basically remained the same for decades. In fact in can be tracked back to the seminal paper by Grosjean and Legrand  from 1960.

What is optical activity and why a commercial CD instrument not always measures CD?

Fresnel was the first to explain optical activity in 1822 by discovering that that right- and left-circularly polarized light propagate with different velocities in an optical active medium medium. The expression he proposed for optical activity is [latexpage]\[

\phi=\pi(n_L-n_R)l/\lambda

\]

where $n_L$ and $n_R$ are, respectively, the (complex) indices of refraction of the medium for left- and right- circularly polarized light. $\lambda$  is the vacuum wavelength of light and $l$ the optical pathlength of the medium.

This equation is  saying that “a medium is optically active if it has different (complex) refractive indices for left and right circularly polarized light”. But this is not equivalent to assuming that one can examine the optical activity of a medium just by sensing circularly polarized light and examining the differential response  . There is a subtle but very important difference!!

The propagation of light in a material is a continuous process, and cannot be presented as a “one-shot” interaction. As light propagates in the medium, the polarization of the wave progressively changes or even disappears due to effects such as linear retardation, diattenuation or depolarization.  A beam of light, initially circularly polarized, changes its polarization as it propagates and, globally, it is refracted or absorbed with an index that is not $n_R$ or $n_L$. Only in a isotropic optically active media the circular polarization is a eigenmode of propagation, which means that the circular polarization is preserved everywhere in the pathlength. This is the only case where the method outlined above to measure circular dichroism works. In all other cases it is advisable to use polarimetric solutions based on the determination of the Mueller matrix.

Application of Mueller matrix polarimetry to the measurement of CD

The  Mueller matrix (M) is a 4×4 matrix of real elements that completely describes the linear optical response of a material. Polarimeters serve to measure one or more elements in M. For instance, commercial CD spectropolarimeters, that have the limitations that we have commented above deliver, the Mueller matrix elements M₀₃ by modulating the input light polarization with a single photoelastic modulator.

For  nondepolarizing materials, the Mueller matrix has at most seven parameters parameters and it can be formulated as follows:\[

\mathbf{M}=\exp(\mathbf{L})=\exp\left(
\begin{array}{cccc}
A &-LD  & -LD’  &  CD\\
-LD &  A & CB  & LB’  \\
-LD’ & -CB &  A& -LB  \\
 CD & -LB’  & LB  & A  \\
\end{array}
\right)
\],

where L is the differential Mueller matrix.  For transmission measurements in a medium homogenous along the direction of propagation of light the entries of L allow for a very simple but very fundamental physical interpretation:

• CD: Circular dichorism
• CB:Circular birefringenge (twice to optical rotation)
• LD: Horizontal linear dichroism
• LB: Horizontal linear birefringence
• LD’: 45º linear dichroism
• LB’: 45º linear birefringence
• A: Absorbance

If M is known from experiment, L can be inverted numerically as  With knowledge of M, Eq. 1 can be inverted numerically by taking the matrix logarithm as $\mathbf{L} = Ln\mathbf{M}$,  or analytically following the method described here. In the case of depolarization, the symmetry of L may be broken because the Mueller matrix will have more independent parameter . In such cases the optical properties can be taken as the average values of related elements  (e.g.  $CD=(L_{03}+L_{30})/2$, $CB=(L_{12}-L_{21})/2$, etc) .

The instrumental approach for a reliable CD

I tend to recommend CD measurements based on the complete determination of the Mueller matrix. By trying to oversimplify the CD measurements, we have reached a point where the user of a CD apparatus all that needs to do is pushing a button to get a nice, sometimes over-smoothed, CD spectra. But  with only this information is almost impossible to figure out if the instrument is “lying” or not, i.e. if the provided CD is CD or it arises from the combination of linear effects.

I pioneered some instruments based on the determination of the Mueller matrix that are very suitable for CD analysis :

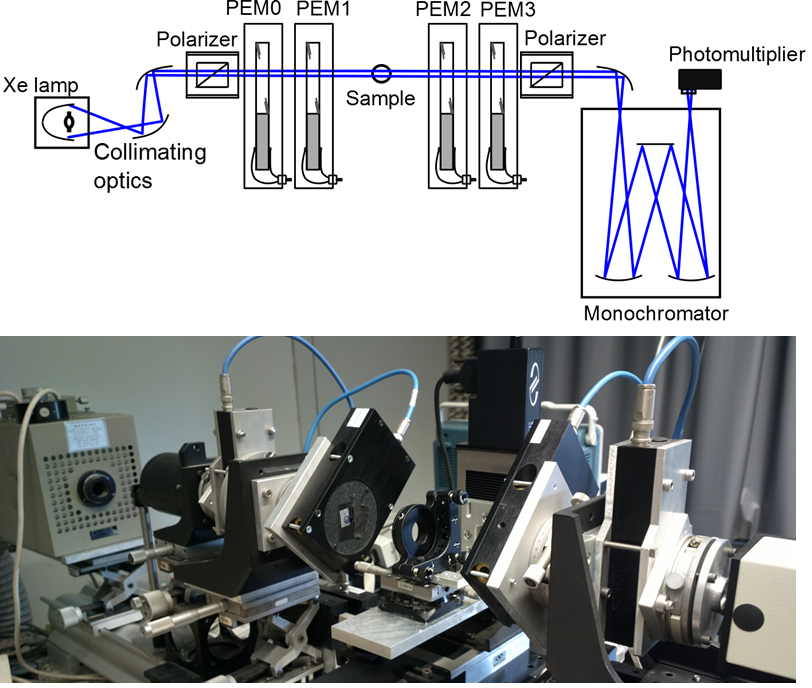
• For spectroscopic measurements: The 4-PEM polarimeter. Click here
• For space resolved measurement: The Mueller matrix microscope: Click here

This is the basic optical design and a photo of the 4-PEM polarimeter: